Here's an analysis of why Aaron (or anyone else) is doomed to failure on this goal. First, define a city-edge to be any city-colored edge of a tile. A given tile can have from zero to four city-edges. Now for all the cities to be self-contained, every city-edge must abut another city-edge. That means the total number of city-edges across all the tiles must be even. But as Aaron showed, in fact the total number of city-edges in the basic set of tiles is odd. So no matter how you re-arrange the tiles, you won't be able to achieve the goal.
This is an example of a parity argument. We can prove that a
given construction is impossible, without considering every
possibility, because the parity of the solution is different from the
parity of all possible arrangements. That's a good thing, because for
each 72-tile rectangle there are 72! × 472 possible
arrangements: over 10147, or way more than the number of atoms in the universe.
The most famous example of a
parity problem is the mutilated
chessboard problem.
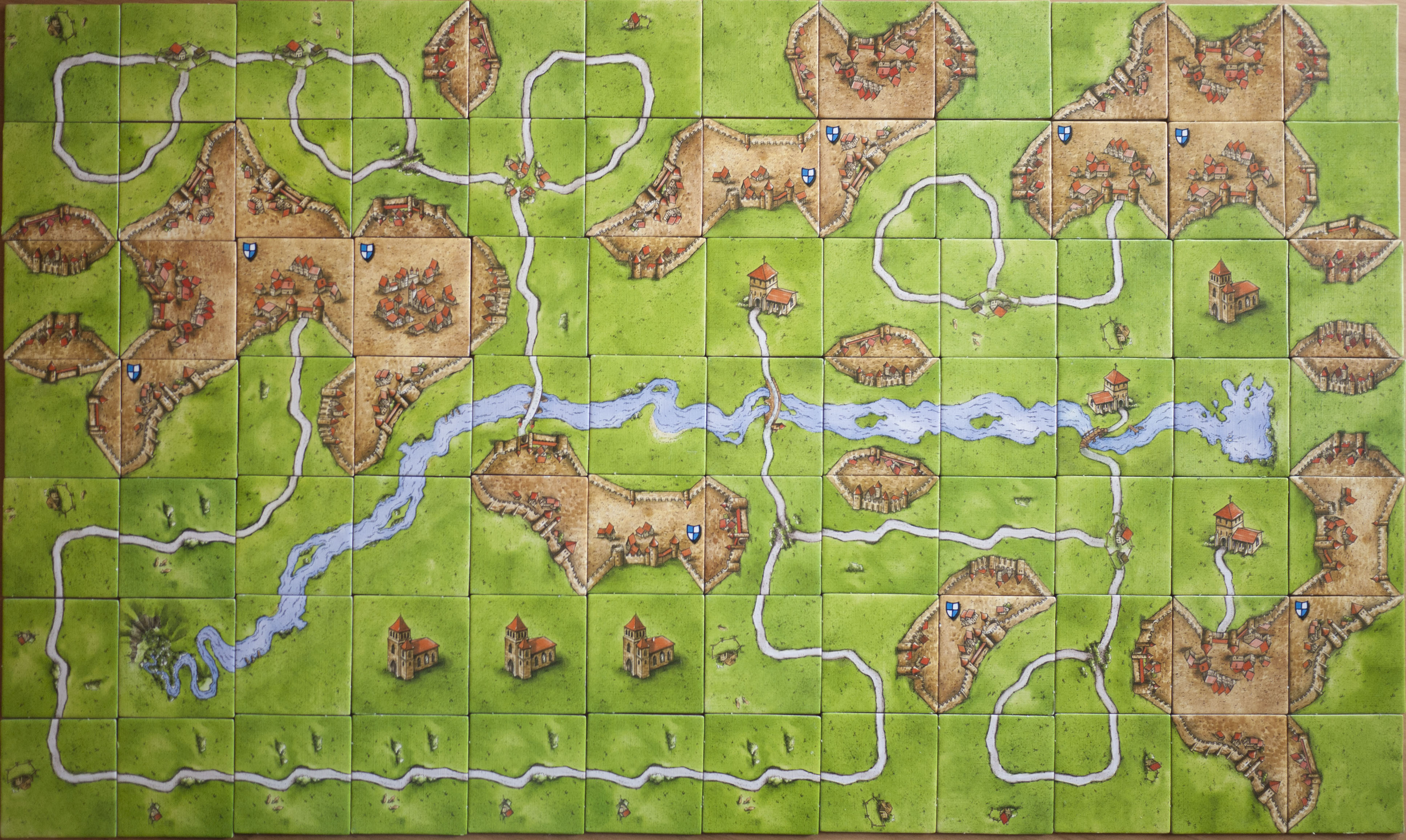
There is a happy ending, however. We have the River Expansion Tiles for Carcassonne: a set of 12 additional tiles that contain river pieces, and happen to contain an odd number of city edges (3). Adding odd and odd we get an even total, and now it is theoretically possible to achieve the goal. (The total number of road-edges is also even, another requirement for achieveing the goal.) In a half hour or so, we were able to get this map:

I'm mostly happy with this. In the lower right there is one abbey that is upside-down and one sideways; I'd like them to be oriented rightside-up. In retrospect I'd like more cities to be closer to the river, although I thought it would be easier to use the river tiles as an edge. Thanks to Emmanuel Delaborde for explaining how to use the Photoshop Transform/Distort command to make this image more nearly rectangular.

Again, I'm mostly happy with the result. The river starts in the mountains of the north and flows south. There is a clear distinction between the big cities of the north and the small ones of the southwest (although there are the medium twin-cities in the southeast). We retain the beautiful two-bridge approach to the river abbey, and then have a big abbey district in the south (making comparison shopping easier). The monks are apparently NASCART fans, because they have an oval racetrack on the southern border. The city folk in the North are more into figure-eight racing.
For next time, here are some more challenges: